4. Effetti della fibra sugli impulsi luminosi

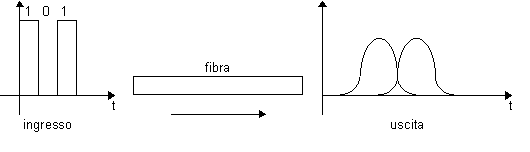
Nel caso di trasmissioni numeriche l'allargamento degli impulsi luminosi che transitano lungo la fibra limita la frequenza massima di lavoro. Infatti, come si mostra in fig.5, ciascun impulso di entrata subisce attenuazione, ritardo e allargamento. In particolare, nel caso di impulsi temporalmente vicini si può avere la parziale sovrapposizione dei segnali uscita, fenomeno noto come interferenza intersimbolica, che compromette la corretta rivelazione dei dati.

Per ridurre la dispersione modale occorre rendere gli indici di rifrazione n₁ e n₂ molto vicini tra loro. Al limite, se n₁ = n₂, si avrebbe a_L = 90° e quindi la luce si può propagare lungo la direzione dell'asse. In questo caso esiste una sola direzione di propagazione e quest'ultima si dice monomodale. Se n₁ è diverso da n₂ esistono più modi di propagazione e quest'ultima si dice multimodale.

La propagazione monomodale si può ottenere anche con n₁ diverso da n₂ ma rendendo il diametro del core molto piccolo e paragonabile alla lunghezza d'onda della radiazione usata. Nella propagazione monomodale, però, si penalizza l'apertura numerica. Al solito, si ricorre ad un compromesso. I valori tipici degli indici di rifrazione sono n₁=1.48 e n₂=1.46 per i quali si ha:

Riflettanza della luce

Quando un raggio luminoso incide sul core della fibra ottica, parte dell'energia associata si trasmette entro la fibra e parte è inevitabilmente persa per riflessione.

Il coefficiente che esprime tale perdita è detto riflettanza r , definito come il rapporto tra la potenza riflessa P_r e quella incidente P_i:

 r = P_r/P_i 

Per ottenere una espressione analitica di r è necessario introdurre il concetto di impedenza caratteristica Z_n del mezzo. Tale impedenza è definita dal seguente rapporto:

Z_n = Z_o / n

  dove:

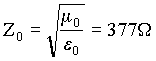
è l'impedenza caratteristica dello spazio ed n è l'indice di rifrazione del mezzo.

Quando un fascio di luce, che si propaga in un mezzo di indice di rifrazione n₀, incide su un secondo mezzo con indice di rifrazione n₁, si ha riflessione e rifrazione.

In particolare il coefficiente di riflessione r_E, definito come il rapporto tra il campo elettrico riflesso E_r ed incidente E_i, vale:

Poiché la potenza associata ad un'onda elettromagnetica è proporzionale al quadrato dell'intensità del campo elettrico, la riflettanza r risulta:

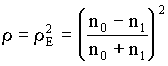
Nel caso della fibra ottica si ha: n₀=1 (aria) e n₁ è l'indice di rifrazione del core, per cui:

 
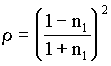
Si conclude che il 3.7% della potenza dell'onda incidente sul core è persa per riflessione.